In computer science, there are many cache algorithms in order to optimize the cache of information stored on the computer.
Normally, there is limited capacity for the cache allocated on the computer, and the computer needs to update the cache or delete the cache if the cache is full. There are many common algorithms for optimizing cache on a computer like: FIFO (First in first out), LFU (Least frequently used), LRU (Least recently used).
Today we are focusing on implementing the LRU (Least recently used) cache algorithm.
I will be using this problem 146. LRU Cache from LeetCode as the guideline for the implementation. Basically, we need to implement the following class:
class LRUCache: def __init__(self, capacity: int):
def get(self, key: int) -> int:
def put(self, key: int, value: int) -> None:
# Your LRUCache object will be instantiated and called as such:# obj = LRUCache(capacity)# param_1 = obj.get(key)# obj.put(key,value)Analyze
A rough thought is that we need to maintain a list-like data structure to store the cache sequentially, and update the list accordingly after each get or put operation.
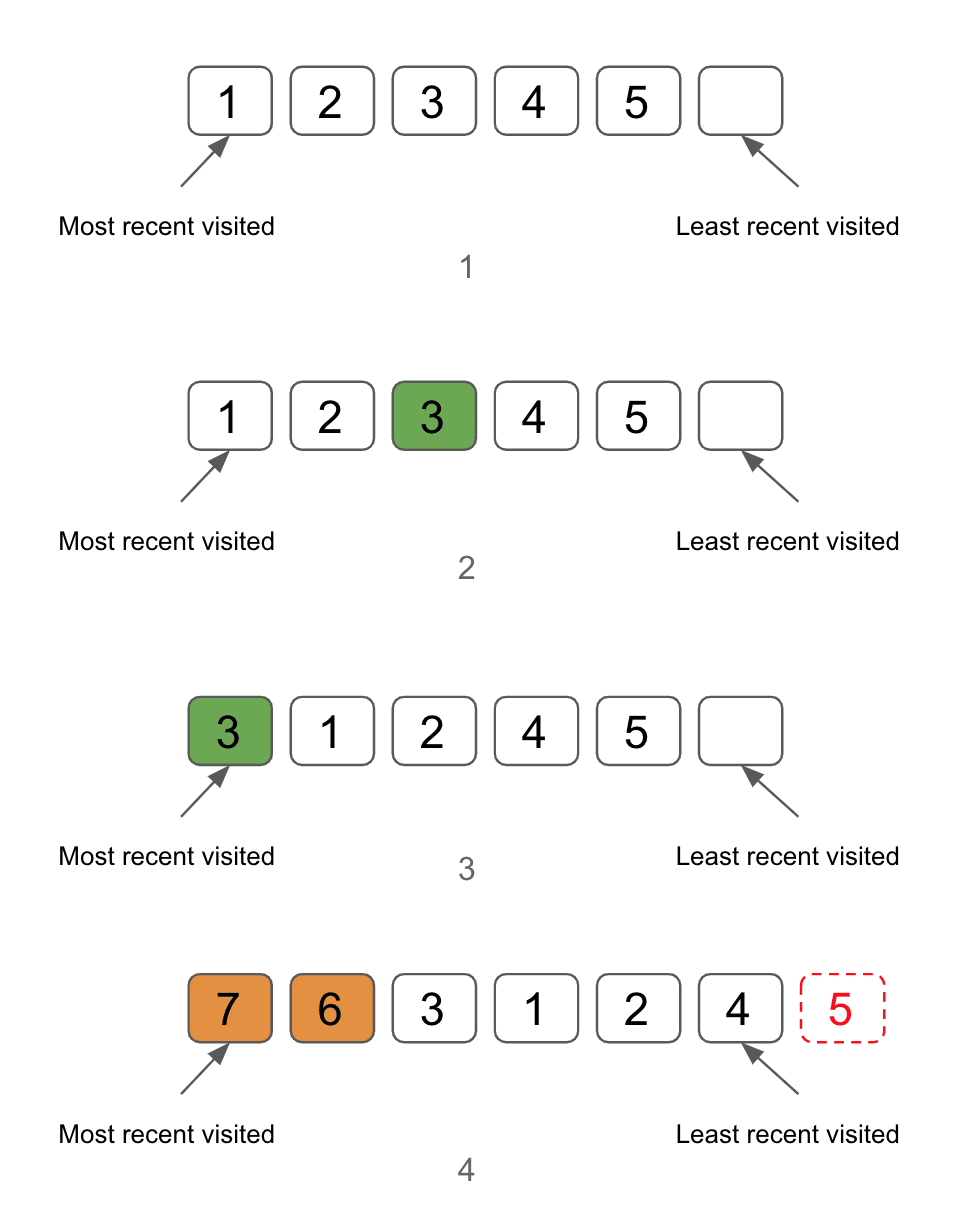
The data towards the end of the list is visited earlier and the data at the beginning is the most recent visited one.
Here is a list represents the cache. It has the capacity of 6, in which 5 of them are filled with data(1).
-
If 3 got visited(2), it will be moved to the beginning of the list(3).
-
If we put 6 and 7 into the cache, 5 will be moved out of the cache since it reaches the capacity of the cache(4).
Using Array
Using an array is pretty straightforward. We have defined a few properties to the class:
cacheData: a dictionary to store the key and valuecacheKey: an array to store only the keys in a specific order
class LRUCache_Array: def __init__(self, capacity: int): self.capacity = capacity self.cacheData = {} self.cacheKey = []
def get(self, key: int) -> int: if key in self.cacheData.keys(): # check if the data already in the cache if key in self.cacheKey: # remove the key from cacheKey self.cacheKey.remove(key) # add the key back to cacheKey at the begining of the array since it is visited self.cacheKey = [key] + self.cacheKey # return the value of the data from the cacheData dictionary return self.cacheData[key] return -1
def put(self, key: int, value: int) -> None: if key in self.cacheData.keys(): # if key already in the cacheData, update the value of the data self.cacheData[key] = value # move the key from cacheKey to the beginning of the array if key in self.cacheKey: self.cacheKey.remove(key) self.cacheKey = [key] + self.cacheKey else: # if the key not in cacheData yet, we need to check if the cacheData exceeds the capacity first before we put the data into the cache if len(self.cacheData) < self.capacity: # add the data to cacheData, and insert the key at the beginning of the cacheKey array if there is still room self.cacheData[key] = value self.cacheKey = [key] + self.cacheKey else: # if exceeds the capacity, remove the last key from cacheKey and delete the data from cacheData. lastDataKey = self.cacheKey.pop() del self.cacheData[lastDataKey] # then insert the data and the key self.cacheData[key] = value self.cacheKey = [key] + self.cacheKeySince we are manipulating the key in an array, for example remove or concatenation, the time complexity of those operations is O(n). And the lookup time on a dictionary in Python is O(1). So the time complexity of each operation(get and put) in this implementation will be O(n).
Using Doubly Linked List
For the doubly linked list, we will need to define an extra ListNode class, which has prev and next pointing to its previous node and next node respectively.
# define the double linked-list nodeclass ListNode: def __init__(self, key = None, value = None): self.key = key self.value = value self.next = None self.prev = NoneThen we will need to define a few properties in our implementation:
cacheData: a dictionary to store the key and valuehead: a head node pointing to the first node of the linked list, initialized asNonetail: a tail node pointing to the last node of the linked list, initialized asNone
# Used double linked-list to maintain the node. O(1)class LRUCache_LinkedList: def __init__(self, capacity: int): self.capacity = capacity self.cacheData = {} self.head: ListNode = None self.tail: ListNode = None
def get(self, key: int) -> int: node = self.cacheData.get(key) if node: # move the current node to the front of the linked list self.__moveNodeToFront(node) return node.value return -1
def put(self, key: int, value: int) -> None: node = self.cacheData.get(key) if node: # key already exsit in cache, update the value node.value = value # move the node to front since it has been updated self.__moveNodeToFront(node) else: newNode = ListNode(key, value) self.cacheData[key] = newNode self.__addNodeAtFront(newNode) if len(self.cacheData) > self.capacity: del self.cacheData[self.tail.key] self.__removeNode(self.tail)
def __moveNodeToFront(self, node: ListNode): self.__removeNode(node) self.__addNodeAtFront(node)
def __removeNode(self, node: ListNode): # This method needs to consider if the node you want to remove is the head or the tail. n = node.next # if node is tail, then n will be None p = node.prev # if node is head, then p will be None if not p: self.head = n node.next = None if n: n.prev = None else: p.next = n if n: n.prev = node.prev else: self.tail = node.prev node.prev = None
def __addNodeAtFront(self, node: ListNode): if not self.head: # if the linked list does not exist yet self.head = node self.tail = node return node.next = self.head self.head.prev = node node.prev = None self.head = nodeSince the time complexity of insertion or deletion operation on a doubly linked list is O(1), and the lookup time on a dictionary in Python is O(1). So the time complexity of each operation(get and put) in this implementation will be O(1).